En las matemáticas puras, las ecuaciones diferenciales se
estudian desde perspectivas diferentes, la mayoría concernientes al conjunto de
las soluciones de las funciones que satisfacen la ecuación. Solo las ecuaciones
diferenciales más simples se pueden resolver mediante fórmulas explícitas; sin
embargo, se pueden determinar algunas propiedades de las soluciones de una
cierta ecuación diferencial sin hallar su forma exacta.
Si la solución exacta no puede
hallarse, esta puede obtenerse numéricamente, mediante una aproximación
usando computadoras. La teoría
de sistemas dinámicos hace énfasis en el análisis
cualitativo de los sistemas descritos por ecuaciones diferenciales, mientras
que muchos métodos numéricos han sido desarrollados para
determinar soluciones con cierto grado de exactitud.
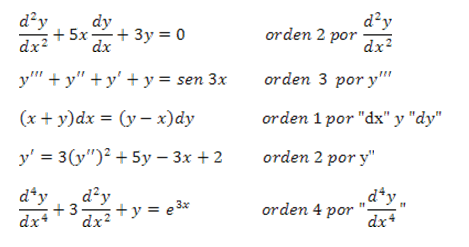
Una ecuación es
una relación entre una serie de variables F(x, y, z, ...)=0.
Por ejemplo:
Expresa
que las variables x e y guardan una
relación en la forma gráfica de una elipse, en el plano OXY.
Las
ecuaciones surgen en Matemáticas cuando se realiza el estudio de un fenómeno
físico, siendo las variables x,y,... ciertas magnitudes físicas
(espacio, tiempo, velocidad, etc.). En ocasiones, al hacer un estudio físico no
sólo aparece una dependencia entre las magnitudes sino que también pueden
aparecer en ella sus derivadas.
Veamos un ejemplo práctico:
Desde una gran altura se deja caer un objeto de masa m .
Queremos determinar la velocidad de caída de este objeto en función del
tiempo t:
La
segunda ley de Newton nos indica que la suma de fuerzas que actúan sobre la
masa será igual a su variación de momento lineal, por tanto:
Siendo g la
aceleración de la gravedad, k el coeficiente de fricción con
el aire, y m la masa del objeto, es decir, g, m y k son
constantes numéricas conocidas. Esta es una ecuación diferencial del
tipo F(v(t), v, v’ ) = 0.
Para
esta ecuación es fácil comprobar que toda función v(t) de la
forma:
Cumple
las condiciones de la ecuación, donde C es cierta constante indeterminada. A
esta función v(t) se la llama solución general de la
ecuación diferencial.
Dependiendo
de las condiciones iniciales del problema podemos hallar diversas soluciones
particulares, en nuestro ejemplo la velocidad inicial es nula (caída libre),
por lo tanto: v(0)=0. Es decir,
Y
por tanto el valor de C, para este caso particular es
Y al
sustituir en la ecuación general obtenemos:
Que
es la solución particular que buscábamos.
Se
trata de una relación entre una variable x, la función
buscada y(x) así como cualesquiera de sus derivadas, y‘(x),
y”(x), ..., yn)(x) .
Simbólicamente
lo expresaremos:
F(x,
y(x), y’(x), y”(x), ..., yn)(x))=0
El
orden de la derivada máxima que interviene en la ecuación se define como orden
de la ecuación. Por ejemplo:
Se
llama grado de la ecuación diferencial al máximo exponente al que se
encuentra elevada la máxima derivada, aunque en numerosas ocasiones sea 1, como
en los dos ejemplos de arriba, éste puede ser cualquier número entero. Por
ejemplo:
Se
trata de una ecuación diferencial de segundo orden, grado
3.
Es conveniente señalar que la solución general de una ecuación diferencial de
primer orden vendrá dependiente de una constante indeterminada, en el caso de
las de segundo orden dependerá de dos constantes, tres para las de tercer
orden, etc.
* Solución general.
Es
toda función y=f(x) que al sustituirla en la ecuación
diferencial F(x, y, y’,...)=0 la convierte en una identidad. A
veces, también es llamada Integral general.
Ejemplo:
Supongamos la ecuación diferencial de segundo orden (grado 1):
Como pronto veremos, su solución general
puede ser expresada en la forma:
y(x) = C1 sen x +
C2 cos x
Comprobemos que esto en efecto es así:
y" = -C1 sen x -
C2 cos x
Al sustituir estos resultados de y", y en la ecuación diferencial, nos encontramos con la identidad:
Lo cual nos asegura que esta y(x) es
en efecto la solución general.
Se trata de ecuaciones de la
forma F(x, y(x), y’(x))=0 . Su solución general es de la
forma y=f(x, C), aunque no siempre es posible expresar esta
solución resuelta respecto a x, en muchas ocasiones la solución
simplemente quedará como f(x, y,C)=0 que dibujadas
gráficamente forman toda una familia de curvas en el plano OXY.
Las condiciones inciales -una sola condición en este caso- viene dada por:
y(xo) = xo
lo
cual geométricamente equivale a dar un punto Po(xo, yo) ,
por el cual sólo pasa una única curva (una solución particular) de la familia
de curvas dada por la solución general.
*
* *
Como un ejemplo consideremos la ecuación
diferencial:
su solución general es:
Esta solución es toda una familia de curvas,
tal como se aprecia en la gráfica adjunta (las curvas -hipérbolas en este caso-
se van obteniendo dando diversos valores a C).
De entre éstas solo existe una solución particular que
cumple la condición y(1)=4, es decir, sólo una hipérbola pasa por
el punto P(1,4), como se ve en la gráfica. Matemáticamente esto lo
haríamos sustituyendo en la solución general los valores x=1, y=4:
por
tanto, C = 4, y la solución particular con la condición y(1) = 4 es:
No hay ningún método sistemático para resolver cualquier ecuación que se nos
presente, lo que hay que hacer es clasificar a las ecuaciones diferenciales
en tipos, y resolverlas según el método específico existente para
cada tipo. A partir de ahora estudiaremos su resolución según sea el tipo de
ecuación.
I) Ec. Dif.
Variables separadas:
Se trata de ecuaciones de la forma:
{1}
es decir, en el miembro de la izquierda
aparece y', en el de la derecha aparece un producto de dos
funciones: una dependiente sólo de la x, otra dependiente sólo de
las y. Un ejemplo de este tipo es:
MÉTODO DE RESOLUCIÓN:
Se trata de arreglar de tal forma la
expresión {1} que nos quede en un miembro solamente las x,
y en el otro miembro sólo las y.
{2}
A
continuación integramos ambos miembros, para así obtener la solución general.
{3}
EJEMPLO:
Sea la ecuación diferencial:
que
puede ser expresada en la forma:
y ahora
integramos los dos miembros:
es
decir, y - 3 Ln y = Ln x
+ Ln C (note cómo cuando aparecen
logaritmos es conveniente expresar la constante de integración en la forma Ln C). Lo
cual en forma más
simple: y = Ln Cx y3 ,
o sea, la solución general es:
ey = C x y3
Puede
observarse el caso más simple de ecuaciones diferenciales con
variables separadas puede expresarse así: M(x) dx +
N(y) dy = 0, siendo M(x) una
expresión dependiente sólo de x; N(y) una
expresión sólo dependiente de y. Un caso reducible a
éste es tener una ecuación en la forma:
{4}
Donde
aparece una función dependiente de y multiplicando a M(x),
y una función dependiente de x multiplicando a N(y). En este
caso podemos dividir a toda la ecuación por el producto de ambas funciones,
así:
Con
lo que ya tenemos una ecuación de variables separadas.
Por
ejemplo, sea la ecuación:
(1
+ x) y2 dx + (1 - y) x dy = 0
Dividimos
a toda la ecuación entre el producto x.y2:
o sea:
ecuación que es integrable directamente:
que tiene por solución general:
Información tomada de una página de referencia.

buena informacion, muy clara y detallada
ResponderEliminar